Unidad 2

Ángulos entre paralelas cortadas por una secante

Ángulos entre rectas paralelas y una secante: en geometría son los ocho ángulos formados por dos rectas paralelas y una transversal a ellas. Estableciendo una relación a distancia entre los ángulos que son formados.

Competencias especificas:

• Razona y argumenta: Distingue las nociones de horizontalidad, verticalidad, paralelismo y perpendicularidad.
• Identifica y construye ángulos: correspondientes, alternos internos, alternos externos y opuestos por el vértice.
• Identifica las propiedades de los diferentes tipos de ángulos estudiados y las aplica en la resolución de problemas.
• Comunica: Usa la simbología propia de ángulos, pares ordenados, y las diferentes posiciones de dos o más rectas.
• Modela y representa: Representa con lenguaje matemático y gráficamente segmentos y diferentes ángulos estudiados, pares ordenados y figuras geométricas en el plano cartesiano.
• Realiza construcciones de ángulos.
• Resuelve problemas: Resuelve problemas para cuya solución se apliquen las diferentes propiedades y relaciones existentes entre los ángulos alternos internos, ángulos alternos externos, ángulos correspondientes y ángulos opuestos por el vértice.
• Utiliza herramientas tecnológicas: Construye rectas perpendiculares, paralelas, bisectrices de ángulos, usando instrumentos apropiados o dispositivos electrónicos.

Indicadores de logro:

Al finalizar esta actividad el estudiante será capaz de:

• Estimar de forma aproximada medidas de segmentos y de ángulos dados y las verifica con la regla y el transportador.
• Estimar de forma aproximada medidas de ángulos dados y las verifica con el transportador.
• Realizar el cálculo mental de la medida del complemento y suplemento de un ángulo, en grados, minutos y segundos.
• Construir rectas paralelas y perpendiculares, bisectriz de un ángulo y mediatriz de un segmento utilizando regla, transportador y compás.
• Identificar puntos del plano dados sus pares ordenados (abscisa, ordenada) de números enteros y fraccionarios usando papel cuadriculado.
• Identificar ángulos: correspondientes, alternos internos, alternos externos y opuestos por el vértice.

-Indicaciones para el lector:

     Bienvenidos nuevamente a nuestro blog, dentro hay distintas actividades las cuales están organizadas desde la más sencilla a la más compleja, las mismas ayudarán a que los estudiantes aprendan y poner en práctica el concepto: Ángulos entre paralelas. 

-Duración de las actividades: 2 semanas de clases.

Actividades:

Para comenzar esta hermosa unidad hagamos un pequeño repaso sobre los ángulos y sus tipos, en la siguiente página interactiva encontrarás lo que debes hacer.

• Nombre de la actividad: Rectas paralelas, transversales y ángulos.

Descripción: Escribe en tu cuaderno los conceptos de: ángulos, rectas paralelas y rectas transversales, como se forman los ángulos alternos internos y alternos externos. 

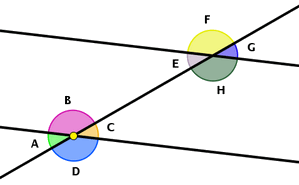
Observa la imagen e identifica los ángulos opuestos por el vértice, alternos internos, alternos externos y correspondientes.

Razone y argumente para responder las siguientes preguntas:

     ¿Cómo se forman los ángulos correspondientes?

     ¿Qué características tienen los ángulos opuestos por el vértice?

     ¿Qué son los ángulos alternos internos y alternos externos? 

• Nombre de la actividad: Identifique y escriba con cuales colores se forman ángulos correspondientes, alternos internos, alternos externos y opuestos por el vértice.

• Nombre de la actividad: Medida de ángulos.

Recuerda que es un transportador y como se utiliza viendo los vídeos enlazados y analiza la diferencia entre ángulos complementarios y suplementarios. Esto facilitará que realices las siguientes mediciones y encuentres el complemento y suplemento de cada ángulo dado según sea necesario.

• Nombre de la actividad: Construyo rectas en el plano cartesiano.

Descripción: Sea creativo y construya dos rectas en el plano cartesiano que sean paralelas entre sí, y que a su vez sean cortadas por una secante. Pueden utilizar desde los clásicos lápiz y papel, transportador y regla hasta cualquier software de computadora o móvil como geogebra clásico, geogebra geometría, scilab, genius entre otros. Miren este ejemplo para que se ilustren de como lo pueden hacer Ángulos entre paralelas.

Luego entre a kahoot para responder las preguntas que tienen a continuación sobre lo que observan en las gráficas que crearon. Link para el docente kahoot.

PREGUNTAS

1. ¿Cuáles de los siguientes pares de ángulos son opuestos por el vértice? -¿Qué relación guardan entre sí los ángulos opuestos por el vértice?
2. El ángulo A y el ángulo E son adyacentes. -¿Qué relación guardan entre sí los ángulos adyacentes?
3. Los ángulos < 1 y < 5 son.
4. Los ángulos alternos internos en el siguiente gráfico son. -¿Qué relación mantienen entre sí dos ángulos alternos internos?
5. Una pareja de ángulos alternos externos que hay en el gráfico es. -¿Qué relación mantienen entre sí dos ángulos alternos externos?
6. ¿Qué sucedería si la recta que corta a las dos rectas paralelas fuera perpendicular a ellas?
7. Los ángulos A y B son conjugados externos.

• Nombre de la actividad: Resuelve problemas

Descripción: Resuelve los siguientes problemas con los conocimientos ya adquiridos sobre el tema tratado en esta unidad. Entra a este link y luego de resolver indique que propiedad utilizó para llegar a su respuesta.

Diviértete con las actividades extras:

Infórmate con estas imágenes: